Wie funktioniert das Buli-Orakel?
Das Buli Orakel liefert dir die statistisch optimalen Tipps für deine Kicktipp Runde basierend auf den Wettquoten der Buchmacher und den Punkteregeln deiner Kicktipp Runde. Wenn du dich an die Tipps hältst, dann landest du mit hoher Wahrscheinlichkeit weit vorne in deiner Tipprunde!
Das bedeutet jedoch NICHT, dass das Buli-Orakel tatsächlich den Ausgang des Spiels voraussagen könnte, oder dir den Sieg garantiert. Es berechnet stattdessen diejenigen Tipps, die langfristig die meisten Punkte liefern sollten. Kurzfristig ist es natürlich immer möglich, dass glückliche Außenseiter-Tipps besser fahren!
Das Tolle am Buli Orakel: Da jede Kicktipp Liga ihre Regeln selbst bestimmen kann, gibt es keinen universellen perfekten Tipp. Wenn deine Runde z. B. Auswärtssiege besonders belohnt, kann sich ein 1:2 Tipp auf die Auswärtsmannschaft lohnen, obwohl bei anderen Regeln der Tipp auf einen Heimsieg vielversprechender wäre!
Das Buli Orakel nimmt dir diese Entscheidung ab und liefert den perfekten Tipp für deine persönliche Liga!
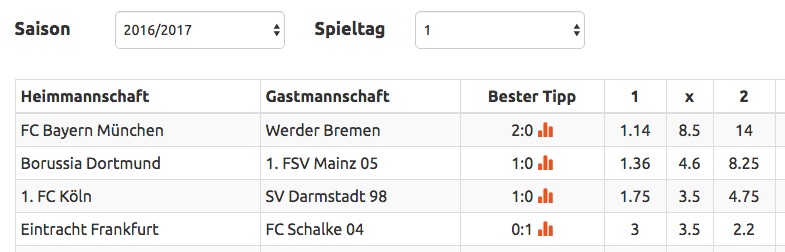
Deine optimalen Tippvorschläge...
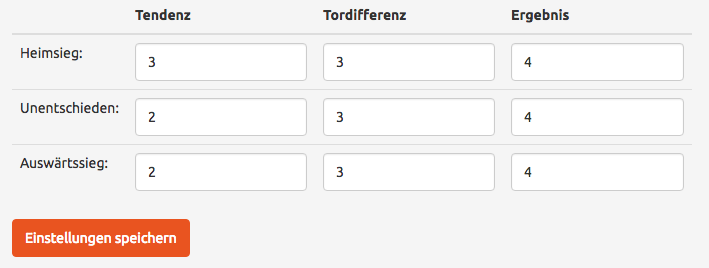
... basierend auf deinen Spielregeln
Wie berechnet Buli Orakel die optimalen Tipps?
Im ersten Schritt werden die Wettquoten der Buchmacher vor dem Spiel benötigt. Dabei sind die Quoten von diesen zwei Wetten von großem Interesse:
Die Siegwette:
Die Quoten für einen Heimsieg, ein Unentschieden oder einen Auswärtssieg liefern die Information welche Mannschaft favorisiert wird und wie groß der Leistungsunterschied zwischen beiden Mannschaften ist.
Die Anzahl der Tore:
Die Wettquoten für mehr oder weniger als 2.5 Tore zeigen uns wieviele Tore die Buchmacher für das Spiel erwarten.
Was genau sagen uns die Quoten?
Wenn wir eine Aussage über den perfekten Tipp treffen wollen, müssen wir zuerst die Wahrscheinlichkeit jedes einzelnen Spielausgangs berechnen. Das heißt, wir müssen kalkulieren wie wahrscheinlich ein 0:0, 1:0, 1:1 , 0:1 usw ist.
Und Achtung, hier kommt die Statistik ins Spiel:
Man kann zeigen, dass die Tore die in einem Fußballspiel fallen (annähernd) poissonverteilt sind.
Die folgende Grafik zeigt die tatsächliche Toreverteilung in der 1.Bundesliga seit der Saison 2005/2006, verglichen mit der Poisson-Verteilung:
Torverteilung in der 1.Bundesliga seit 2005/2006
| Tore pro Spiel | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Beobachtete Häufigkeit: | 6.84% | 14.43% | 23.88% | 22.25% | 16.03% | 9.27% | 4.89% | 1.39% | 0.68% |
| Poisson Verteilung mit λ= 2.87: | 5.67 | 16.27 | 23.35 | 22.34 | 16.03 | 9.2 | 4.4 | 1.8 | 0.65 |
Die Poisson Verteilung ist eine einparametrische Verteilung. Das heißt, wir müssen nur einen Wert λ bestimmen (die erwartete durchschnittliche Toranzahl) und können die Wahrscheinlichkeit jeder Toranzahl berechnen.
In den Bundesligaspielen seit der Saison 2005/2006 sind im Schnitt 2.87 Tore gefallen. Die Grafik zeigt eine generell sehr gute Übereinstimmung zwischen der beoachten Verteilung der Tore und der theoretischen Poisson Verteilung. Nur die Spiele ohne Tore sind etwas überrepräsentiert (6.84% vs 5.67%) und Spiele mit genau einem Tor etwas seltener als erwartet (14.43% vs 16.27%). Für Spiele mit mehr als einem Tor ist die Übereinstimmung erstaunlich gut!
Das bedeutet: wenn wir den Erwartungswert der Tore für eine Mannschaft schätzen können, dann erlaubt uns die Poissonverteilung die Wahrscheinlichkeit zu berechnen, dass die Mannschaft 0,1,2,3… Tore schießt.
Um das Konzept verständlicher zu machen, will ich es an einem Beispiel erklären:
Schritt 1: Bestimmung der erwarteten Tore
Nehmen wir uns als Beispiel das Eröffnungsspiel der Saison 2016/2017:
Wettquoten für FC Bayern München: Werder Bremen
| Siegwette | Quote |
|---|---|
| FC Bayern München | 1.08 |
| Unentschieden | 11.5 |
| Werder Bremen | 25 |
| Over / Under | Quote |
|---|---|
| < 2.5 Tore | 4 |
| > 2.5 Tore | 1.25 |
Die Wette, dass weniger als 2.5 Tore fallen hatte eine Quote von 4. Das heißt, man hätte das Vierfache seine Einsatzes ausbezahlt bekommen wenn zwei Tore oder weniger gefallen wären.
Aus dieser Quote lässt sich berechnen dass die Buchmacher mit einer Wahrscheinlichkeit von 23.81% annahmen, dass zwei oder weniger Tore fallen. ( Wkt= (1/4)*95% Auszahlungsqoute)
Die erwartete Anzahl der Tore lässt sich nun berechnen, indem wir den Parameter λ einer Poisson Verteilung finden, sodass die Wahrscheinlichkeit von maximal 2 Toren diesen 23.81% entspricht.
Das Prinzip wird deutlicher in diesem interaktiven Chart einer Poisson Verteilung. Durch Verändern des Parameters λ könnt ihr euch verschiedene Verteilungen und die dazugehörigen Wahrscheinlichkeiten für <2.5 Tore anschauen:
Poisson Verteilung mit erwartete Tore (λ):
| Erw. Tore | Wkt in % |
| < 2.5 Tore | 23.81% |
| > 2.5 Tore | 76.19% |
| Erw. Tore | Wkt in % |
| 0 Tore | 1.83% |
| 1 Tore | 7.33% |
| 2 Tore | 14.65% |
| 3 Tore | 19.54% |
| 4 Tore | 19.54% |
| 5 Tore | 15.63% |
Ausgehend von den Quoten bei FC Bayern München: Werder Bremenerwarteten die Buchmacher also durchschnittlich ca. 4 Tore.
Nun da wir wissen wie viele Tore im gesamten Spiel erwartet werden, müssen wir diese sinnvoll auf beide Mannschaften aufteilen:
Schritt 2: Verteilen der Tore auf beide Mannschaften
Den Quoten der Buchmacher können wir entnehmen, dass sie Bayern München eine 88% Chance auf einen Sieg einräumen, während Bremen nur eine Chance von 4% hat (8% Unentschieden).
Wir können also davon ausgehen dass Bayern München im Durchschnitt mehr Tore schießt als Bremen, wir wissen aber nicht direkt, wie groß der Unterschied ist.
Die Lösung:
Wir teilen die 4 Tore in einem ersten Schritt so auf, dass Bayern München einen kleinen Vorteil hat. Zum Beispiel schätzen wir 2.1 Tore für Bayern München und nur 1.9 für Werder Bremen.
Unter der Vorraussetzung, dass die Tore beider Mannschaften wiederum poisson-verteilt sind, können wir nun die Wahrscheinlichkeit eines Sieges für den FCB (oder Bremen) berechnen.
Sollte diese Wahrscheinlichkeit mit den Quoten der Buchmacher übereinstimmen, sind wir am Ziel angekommen. Wenn dies nicht der Fall ist, müssen wir die Aufteilung der Tore so lange anpassen bis eine Übereinstimmung erreicht ist.
Diese interaktive Grafik zeigt, wie sich das Verändern der einzelnen Tore auf die Wahrscheinlichkeiten eines Heimsieges, Auswärtssieges oder Unentschieden auswirkt:
Aus den Quoten der Siegwette:
| Quote | |
|---|---|
| FC Bayern München | 1.08 |
| Unentschieden | 11.5 |
| Werder Bremen | 25 |
Aus der Poisson Verteilung
| Tore | |
|---|---|
| Gesamttore: | 4.01 |
| FC Bayern München | |
| Werder Bremen |
Wir sehen also, dass die Wahrscheinlichkeiten aus der Poisson Verteilung, mit denen der Buchmacher übereinstimmen wenn wir annehmen dass Bayern München im Schnitt 3.38 Tore schießt und Werder Bremen nur 0.63.
Nun da wir die Wahrscheinlichkeit jedes Spielausgangs berechnen können, bleibt nur noch ein Schritt übrig:
Schritt 3: Bestimmen des optimalen Tipps:
Um nun den besten Tipp zu bestimmen, berechnet das Buli Orakel für jeden Tipp zwischen 0:0 und 5:5 die erwartete Punktzahl. Dabei werden die persönlichen Spielregeln, sowie die Wahrscheinlichkeiten aller Ergebnisse berücksichtigt.
Um z.B die erwarteten Punkte für den Tipp 3:0 zu bestimmen, werden zuerst alle Ergebnisse angeschaut, für welche dieser Tipp nur die korrekte Tendenz erfüllen würde (alle Siege des FCB, bei denen die Tordifferenz nicht mit der des Tipps übereinstimmt).
Die addierte Wahrscheinlichkeit dieser Ergebnisse ist 68.45% und wird nach den gewählten Spielregeln mit 2 Punkten belohnt. Multiplikation der Punkte mit der Wahrscheinlichkeit ergibt eine erwartete Punktzahl von 1.37für die korrekt getippte Tendenz.
Diese Schritte werden nun mit allen Ergebnissen, welche bei einem 3:0 Tipp die korrekte Differenz erfüllen, durchgeführt. Die addierte Wahrscheinlichkeit, dass das Spiel mit 4:1, 5:2, 6:3 usw. endet, beträgt 7.73% und wird mit 3 Punkten belohnt. Dies entspricht 0.23 erwarteten Punkten.
Zu guter Letzt fehlen noch die Punkte für das Tippen des korrekten Resultats. Die Wahrscheinlichkeit, dass das Spiel 3:0 ausgeht beträgt 11.62% und wird mit 4 Punkten entlohnt was einer erwarteten Punktzahl von 0.46 entspricht.
Letztendlich ergibt die Addition der erwarteten Punkte aller drei Szenarios den finalen Erwartungswert des Tipps.
Um das zu verdeutlichen zeigt die folgende interaktive Grafik die erwartete Punktzahl eines beliebigen Tipps:
FC Bayern München : Werder Bremen
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 1.8% | 1.2% | 0.4% | 0.1% | 0% | 0% |
| 1 | 6.1% | 3.9% | 1.2% | 0.3% | 0% | 0% |
| 2 | 10.3% | 6.6% | 2.1% | 0.4% | 0.1% | 0% |
| 3 | 11.6% | 7.4% | 2.3% | 0.5% | 0.1% | 0% |
| 4 | 9.8% | 6.2% | 2% | 0.4% | 0.1% | 0% |
| 5 | 6.6% | 4.2% | 1.3% | 0.3% | 0% | 0% |
| Tippergebnis | Pkt | Wkt | EP |
|---|---|---|---|
| Korrektes Ergebnis | 4 | 11.62% | 0.46 |
| Korrekte Differenz | 3 | 7.73% | 0.23 |
| Korrekte Tendenz | 2 | 68.45% | 1.37 |
| Keine Punkte | 0 | 12.12% | 0 |
| Gesamtpunkte | 2.07 |
Im allerletzten Schritt muss dann nur noch der Tipp bestimmt werden, der die höchste erwartete Punktzahl liefert!
Die Übersicht der erwarteten Punkte für jeden Tipp lassen sich im Reiter "Alle Tipps" betrachten. Dort sieht man z.B dass die Tipps 2:0 und 3:0 relativ ebenbürtig sind, ein Tipp auf einen Bremer Sieg jedoch (wenig überraschend) weit schlechter abscheidet.